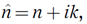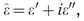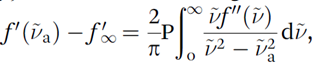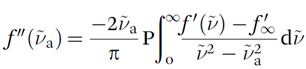ქიმიის ტერმინთა განმარტებითი ლექსიკონი
- ინგლისურ-ქართული
- ქართულ-ინგლისური
- ლექსიკონის შესახებ
- გამოხმაურება

| Kramers–Kronig transforms of a spectrum | სპექტრის კრამერს-კრონიგის გარდაქმნები |
| Analytical chemistry | ანალიზური ქიმია |
Functions based on the physical principle of causality that interconvert the real and imaginary parts of complex optical quantities when they are known over a sufficiently wide (strictly infinite) wavenumber range. They are frequently used to interconvert the real part, f′, and imaginary part, f″, of the refractive index, dielectric constant (relative permittivity), or logarithm of the complex reflection coefficient reiφ through
where P means that the principal part of the integral is taken at the singularity. Note: All functions used to model vibrational spectra obey the Kramers–Kronig transforms as long as the real parts are even functions of wavenumber and the imaginary parts are odd functions of wavenumber so that the Kramers– Kronig transforms are equivalent to the Hilbert transforms. |
მიზეზ-შედეგობრიობის ფიზიკურ პრინციპზე დაფუძნებული ფუნქციები, რომლებიც ურთიერთგარდაქმნის რთული ოპტიკური სიდიდეების რეალურ და წარმოსახვით ნაწილებს, როდესაც ისინი ცნობილია საკმარისად ფართო (მკაცრად უსასრულო) ტალღური რიცხვების დიაპაზონში. ისინი ხშირად გამოიყენება გარდატეხის მაჩვენებლის
დიელექტრიკული მუდმივას (ფარდობითი დიელექტრიკული შეღწევადობის) ან კომპლექსური არეკვლის კოეფიციენტის reiφ ლოგარითმის რეალური ნაწილის f′ და წარმოსახვითი ნაწილის f″ ურთიერთგარდაქმნით შემდეგი ფორმულების საშუალებით სადაც P ნიშნავს, რომ ინტეგრალის მთავარი ნაწილი აღებულია სინგულარობის დროს. შენიშვნა: რხევითი სპექტრების მოდელირებისთვის გამოყენებული ყველა ფუნქცია ემორჩილება კრამერს-კრონიგის გარდაქმნებს, თუ რეალური ნაწილები ტალღური რიცხვის ლუწი ფუნქციებია, ხოლო წარმოსახვითი ნაწილები ტალღური რიცხვის კენტი ფუნქციები, ამიტომ კრამერს-კრონიგის გარდაქმნები ჰილბერტის გარდაქმნების ეკვივალენტურია. |
| Source | წყარო: D. B. Hibbert, Compendium of terminology in analytical chemistry. Cambridge: Royal Society Of Chemistry, 2019 |
|