J. Geo. Chem. Soc., 2021, Vol. 1, Issue: 1, pp. 46 - 51

რნბ-მატრიცის დეტერმინანტის ლოგარითმის წარმოდგენა უნიშნო ლაპლასიანის ფუნქციის სახით: 1. ფუნქციური ჯგუფების წვლილი

გ. ლეკიშვილი^1,*, მ. გვერდწითელი², ი. გუტმანი³

¹თბილისის სახელმწიფო სამედიცინო უნივერსიტეტი
²ივ. ჯავახიშვილის სახელობის თბილისის სახელმწიფო უნივერსიტეტი
³კრაგუევაცის უნივერსიტეტი, სერბია

g.lekishvili@tsmu.edu

Abstract.

რნბ-მატრიცის (Γ) დეტერმინანტის ათობითი ლოგარითმი ფართოდ გამოიყენება “აღნაგობა-თვისება” და “აღნაგობა-ბიოაქტივობა” მოდელირებისას. ნაჩვენებია რნბ-მატრიცის უნიშნო ლაპლასიანის მიხედვით გამოთვლის შესაძლებლობა და მისი ფორმა ნაჯერი ნახშირწყალბადებისათვის: Γ=2I_n + Q რადგან უნიშნო ლაპლასიანი დადებითი ნახევრადგანსაზღვრული მატრიცაა, (Γ) მატრიცის თითოეული საკუთარი მნიშვნელობა დადებითია. შესაბამისად, მისი დეტერმინანტის ლოგარითმი მატრიცის ლოგარითმის კვალს უდრის. სათანადო სპექტრული რადიუსის მქონე დამხმარე მატრიცის გამოყენებამ და მისი ლოგარითმის განვრცობამ ტეილორ-მაკლორენის მწკრივებში იმის გათვალისწინებით, რომ მატრიცის k-ური ხარისხის კვალი k-ურ სპექტრულ მომენტისა და ქვეგრაფების აღმოჩენის სიხშირეების გამოთვლის საშუალებას გვაძლევს,  შემდეგ განტოლებამდე მიგვიყვანა: GG ≈ 0.3663n + 0.2366m - 0.0267|K_1,2| + 0.0005|K_1,3| - 0.000036|D_1,1| - 0.0005|C₃ | - 0.00012|K_1,4| - 0.00004|C_3,1| - 0.000072|C₄| + 0.000008|D_2,1| + 0.000096|K_1,5| + 0.000008|C_4,1| + 0.000008|Φ₁| + 0.000008|C₅| + 0.000016|C_3,2| + 0.000032|Φ₂|

აღსანიშნავია, რომ, პრინციპში, GG ინდექსის აპროქსიმაცია ნებისმიერი სიზუსტითაა შესაძლებელი შესაბამისი სპექტრული მომენტების გამოთვლის კვალდაკვალ.

Keywords: ქიმიური გრაფი, თანაზიარობის მატრიცა, ტოპოლოგიური ინდექსი, უნიშნო ლაპლასიანი, მატრიცის ლოგარითმი

 

შესავალი

რიგობრივი ნომრებისა და ბმების (რნბ-) მატრიცის დეტერმინანტის ათობითი ლოგარითმი ფართოდ გამოიყენება “აღნაგობა-თვისება” და “აღნაგობა-ბიოაქტივობა” კორელაციების შესწავლისას. ამ ტოპოლოგიური ინდექსის მეშვეობით გამოკვლეულია ნაერთთა სხვადასხვა კლასების წარმომადგენელთა ფიზიკური თვისებებისა და ბიოაქტივობის მათ სტრუქტურებზე დამოკიდებულება, მაგალითად, II მთავარი ქვეჯგუფის ელემენტთა ქლორიდების სტანდარტული თავისუფალი ენერგიები [1], ბინარული ნაერთების კრისტალური სტრუქტურების თავისებურებები [2], ნორმალურჯაჭვიანი მონოჰალოგენალკანების დუღილის ტემპერატურები [3], მჟავების დუღილის ტემპერატურები [4], 1-S-ცისტეილაცეტოგლუკოზის სინთეზი [5] და სხვა მრავალი.

უნდა აღინიშნოს, რომ მოდელების წარმატებული გამოყენება დამოკიდებულია მათ ინტერპრეტადობაზე, რაც, თავის მხრივ, განისაზღვრება არა მხოლოდ მოლეკულის აღნაგობის ჰოლისტური წარდგენით, არამედ მასში შემავალი ფუნქციური ჯგუფების ტიპით, რაოდენობით, თვისებებით, ურთიერთგავლენითა და წვლილით. ამრიგად, საჭიროა პირველადი ინვარიანტების სასრული ბაზისის შერჩევა და ტოპოლოგიური ინდექსის წარმოდგენა მათი წრფივი კომბინაციით. პირველადი ინვარიანტების სახით ბუნებრივია ქვეგრაფების (ფუნქციური ჯგუფების ალგებრული მოდელების) მოცემულ გრაფში აღმოჩენის სიხშირეების გამოყენება. ასეთ შემთხვევაში შესაძლებელი ხდება გრაფის ნებისმიერი ინვარიანტის შემდეგნაირი შეფასება:

 

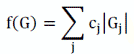
სადაც f(G) G გრაფის ინვარიანტია, |G_j| წარმოადგენს G_j ქვეგრაფის G გრაფში აღმოჩენის სიხშირეს, ხოლო c_j გარკველი სიდიდეა, რომელიც დამოკიდებულია ინვარიანტის ბუნებაზე და არ არის დამოკიდებული G_j ქვეგრაფზე [6]. c_j სიდიდეების შესაფასებლად განსხვავებული მიდგომების გამოყენება შეიძლება [7], მაგრამ უკანასკნელ დროს უპირატესობა ენიჭება გრაფების სპექტრული მომენტებზე დამყარებულ მეთოდებს,  რადგან მათი მეშვეობით ქვეგრაფის აღმოჩენის სიხშირეების გამოთვლა იოლია. რაც შეეხება მათი წვლილის შეფასებას, მატრიცების ფუნქციებისა და მათი ტეილორ-მაკგოვერნის მწკრივების გამოყენება წარმოადგენს ეფექტურ მიდგომას [8].

წინამდებარე ნაშრომი წარმოადგენს რნბ-მატრიცის დეტერმინანტის ლოგარითმის ქვეგრაფების წვლილის მიხედვით შეფასების მცდელობას.

 

ძირითადი ნაწილი

ცნებები და განმარტებები

რიგობრივი ნომრებისა და ბმების (რნბ) Γ მატრიცა შემდეგნაირად განისაზღვრება:

 

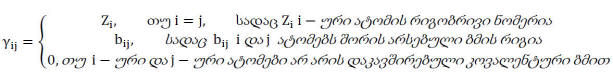
ცხადია, რომ Γ მატრიცა კვადრატულია და სიმეტრიული. ზემოხსენებული სახით Γ მატრიცა აიგება იმ მოლეკულური გრაფების შემთხვევაში, რომლებიც მოიცავენ წყალბადის ატომებს, ხოლო თუ მატრიცას განვსაზღვრავთ წყალბადის ატომების პირდაპირი გათვალისწინების გარეშე, მაშინ მის ელემენტებს შემდეგი სახე ექნება:

γ_i = Z_i-h_i = Z_i + δ_i - v_i   (1a)

γ_ij = a_ij + π_ij  (1b)

სადაც h_i i-ურ ატომთან დაკავშირებული წყალბადის ატომების რაოდენობაა, δ_{i -} წვეროს ხარისხი, ხოლო v_i i-ური ატომის ვალენტობაა. a_ij თანაზიარობის მატრიცის  ელემენტია, π_ij i-ურ და j-ურ ატომებს შორის π-ბმების რაოდენობას წარმოადგენს.

რნბ-მატრიცის დეტერმინანტის ლოგარითმი (GG) შემდეგნაირად გამოითვლება:

GG = lg (det(Γ))   (2)

აღსანიშნავია, რომ GG-ინდექსის მნიშვნელობა არ იცვლება გრაფში წყალბადის ატომების გაუთვალისწინებლობით.

ალგებრულ გრაფთა თეორიის ზოგიერთი ცნება.

მატრიცების დახასიათება შესაძლებელია მათი კვალით:

      (3)

კვადრატული მატრიცის კვალის გამოთვლა შესაძლებელია მატრიცის სპექტრის მიხედვით:

    (4)

სადაც λ_i მატრიცის საკუთარ მნიშვნელობებს წარმოადგენს.

მატრიცის დეტერმინანტის გამოთვლა შესაძლებელია ამავე მატრიცის საკუთარი მნიშვნელობების მეშვეობითაც:

(5)

კვადრატული მატრიცების ფუნქციების შეფასება, ასევე, შესაძლებელია მატრიცის სპექტრის მეშვეობით [9]:

f(M) = V f(Λ)V^T    (6)

სადაც V საკუთარი ვექტორების კონკატენაციით მიღებული ორთონორმალური მატრიცაა, ხოლო Λ - დიაგონალური მატრიცა, რომლის ელემენტებსაც M მატრიცის საკუთარი მნიშვნელობები წარმოადგენს. აღსანიშნავია, რომ [f(Λ)]_ii=f(λ_i). როდესაც რეალური მატრიცის ყველა საკუთარი მნიშვნელობა დადებითია, მატრიცის ნატურალური ლოგარითმი რეალური რიცხვებისაგან შემდგარ მატრიცას წარმოადგენს.

მარტივი გრაფი არ შეიცავს ორიენტებულ ან მრავალჯერად წიბოებს. მისი უნიშნო ლაპლასიანი (Q) შემდეგნაირად განისაზღვრება:

Q = ∆ + A     (7)

სადაც Δ წვეროთა ხარისხებისაგან შედგენილი დიაგონალური მატრიცაა, ხოლო A - თანაზიარობის მატრიცა. მოცემული გრაფის უნიშნო ლაპლასიანი ამავე გრაფის  ინციდენციის მატრიცასა (R) და წიბოგრაფის თანაზიარობის მატრიცასთან  (A_L) მარტივი მიმართებებითაა დაკავშირებული:

Q = RR^T   (8)

R^T R = A_L + 2I     (9)

               რადგან როგორც RR^T, ისე R^TR მატრიცებს ერთი და იგივე არანულოვანი საკუთარი მნიშვნელობები გააჩნია, უნიშნო ლაპლასიანის საკუთარი მნიშვნელობების გამოთვლა წიბოგრაფის სპექტრის მიხედვითაა შესაძლებელი:

ξ_j = λ_j + 2     (10)

სადაც ξ_j უნიშნო ლაპლასიანის, ხოლო λ_j  - წიბოგრაფის j-ური საკუთარი მნიშვნელობაა.

უნიშნო ლაპლასიანის სპექტრული მომენტების (κ_k) წიბოგრაფის სპექტრული მომენტების (μ_k) მეშვეობით გამოსახვა ამგვარად ხდება შესაძლებელი:

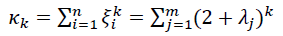  (11)

სადაც n და m გრაფის წვეროებისა და წიბოების რაოდენობაა.

როგორც ცნობილია, უნიშნო ლაპლასიანი დადებითი ნახევრადგანსაზღვრული მატრიცაა და მისი ნულოვანი საკუთარი მნიშვნელობების ჯერადობა გრაფის ბიპარტიტული კომპონენტების რაოდენობას უტოლდება. ალიციკლური ნაჯერი ნახშირწყალბადების გრაფ-თეორიულ მოდელებს ხეები (უციკლო გრაფები) წარმოადგენს; რადგან ხე ბიპარტიტული კომპონენტია, ნებისმიერი ნაჯერი ნახშირწყალადის გრაფს არაუმეტეს ერთი ნულოვანი საკუთარი მნიშვნელობა შეიძლება გააჩნდეს. კენტი რაოდენობის წევრების მქონე ციკლების შემცველ ნაჯერ ნახშირწყალბადებს საერთოდ არ გააჩნია ნულოვანი საკუთარი მნიშვნელობა [10].

შედეგები და მათი განსჯა

Γ მატრიცის შეფასება შესაძლებელია უნიშნო ლაპლასიანის გამოყენებით (იხ. განტოლება 1):

Γ = W + Δ + A = W + Q    (12)

სადაც დამხმარე მატრიცის (W) ელემენტები შემდეგნაირად გამოითვლება:

w_ii = Z_i - v_i   (13a)

w_ij=π_ij   (13b)

მოცემულ სტატიაში დასმული ამოცანის გადასაწყვეტად საკმარისია ნაჯერი ნახშირწყალბადების Γ მატრიცის განხილვა, რაც დამხმარე მატრიცის გამოთვლას გაამარტივებს:

w_ii = Z_i - v_i = 6 – 4 = 2   (14a)

w_ij=0  (14b)

შესაბამისად:

W = 2I_n  (15a)

Γ = 2I­ + Q   (15b)

სადაც I_n წარმოადგენს n×n განზომილების მატრიცას ერთეულოვანი დიაგონალური და ნულოვანი არადიაგონალური ელემენტებით.

            ნათელია, რომ Γ მატრიცა დადებითი განსაზღვრული მატრიცაა:

ω_i = 2 + ξ_i = 4 + λ_i > 0

სადაც ω_i  Γ მატრიცის, ξ_i  - უნიშნო ლაპლასიანის (Q), ხოლო λ_i - წიბოგრაფის (A_L) i-ური საკუთარი მნიშვნელობაა. ამდენად, Γ მატრიცის ლოგარითმის გამოთვლა შესაძლებელია მატრიცის ფუნქციით:

lg (Γ) = V lg(Λ)V^T   (16)

დეტერმინანტის საყოველთაოდ ცნობილი თვისებების მიხედვით გამოდის, რომ

     (17)

მატრიცების ფუნქციების გამოთვლა ტეილორ-მაკლორენის მწკრივების მეშვეობითაც არის შესაძლებელი, თუ მოცემული მატრიცის სპექტრული რადიუსი განაპირობებს მწკრივის კრებადობას:

   (18a)

ასეთ შემთხვევაში, მატრიცის კვალი გამოითვლება სპექტრული მომენტების მიხედვით:

μ_k = Tr(M^k)   (18b)

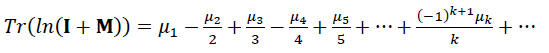   (18c)

სპექტრული მომენტების გამოყენების უპირატესობას წარმოადგენს ის გარემოება, რომ ისინი დაკავშირებულია ქვეგრაფის აღმოჩენის სიხშირეებთან, რაც გრაფის ინვარიანტებში ქვეგრაფების (და, მაშასადამე, ფუნქციური ჯგუფების) წვლილის შეფასების საშუალებას იძლევა.

აღსანიშნავია, რომ მატრიცის ლოგარითმის შემთხვევაში სპექტრული რადიუსი ერთზე ნაკლები უნდა იყოს (ρ(M)<1) [9]. Γ მატრიცის სპექტრული რადიუსის შეფასება უნიშნო ლაპლასიანის მიხედვით შეიძლება. ეს უკანასკნელი დადებითი ნახევრადგანსაზღვრული მატრიცაა, რომლის ნულოვანი საკუთარი მნიშვნელობების ჯერადობა უტოლდება ბიპარტიტული კომპონენტების რაოდენობას, ხოლო წამყვანი (უდიდესი) საკუთარი მნიშვნელობა არ აღემატება  2Δ, სადაც  Δ  წვეროთა ხარისხებს შორის უდიდესია [11]. აქედან შეგვიძლია დავასკვნათ, რომ Γ-I მატრიცის სპექტრული რადიუსი [1,  2Δ+1] ინტერვალშია.

ამრიგად, Γ მატრიცის ნატურალური ლოგარითმის ტეილორ-მაკგოვერნის მწკრივი კრებადი არაა.

ესტრადასა და ბენცის რეკომენდაციის შესაბამისად განვიხილოთ დაყვანილი Γ მატრიცა:

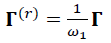  (19)

სადაც ω₁ Γ მატრიცის წამყვანი საკუთარი მნიშვნელობაა და, როგორც ზემოთ (განტოლება 10) აღინიშნა, უნიშნო ლაპლასიანის წამყვანი საკუთარი მნიშვნელობის (ξ₁) მიხედვით გამოითვლება.

Γ^(r)-I მატრიცის სპექტრული რადიუსი   შემდეგი იგივეობის მიხედვით შეფასდება:

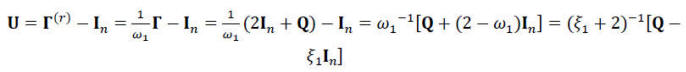  (20)

როგორც ვხედავთ, U=Γ^(r)-I მატრიცის სპექტრული რადიუსი  ინტერვალს მიეკუთვნება და, ამრიგად, აკმაყოფილებს მწკრივის კრებადობის კრიტერიუმს. აღსანიშნავია, რომ დაყვანილი Γ^(r) მატრიცა დადებითი განსაზღვრული მატრიცაა და მისი საკუთარი მნიშვნელობების ნატურალური ლოგარითმები რეალურ რიცხვებს წარმოადგენს.

ზემოთქმულიდან გამომდინარე:

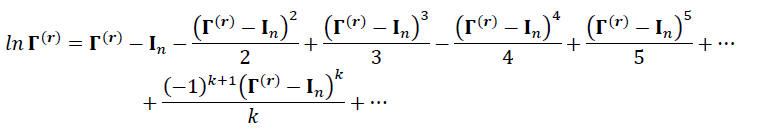(21a)

და

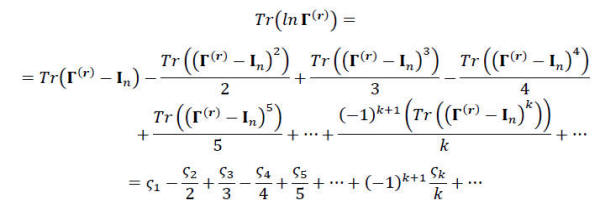(21b)

სადაც   of U =  Γ^(r)  - I მატრიცის სპექტრულ მომენტებს წარმოადგენს:

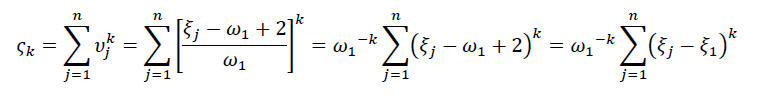(21c)

ნათელია, რომ  ς₁=0 და

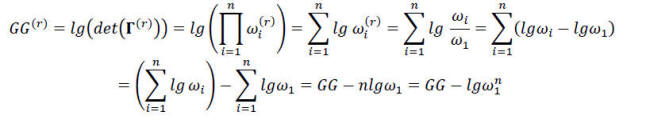(22a)

ამდენად,

  GG = GG^(r) + lgω₁ⁿ       (22b)

საბოლოოდ კი ვღებულობთ:

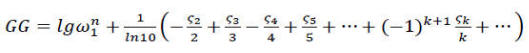   (23)

დაყვანილი მატრიცის სპექტრული     მომენტების უნიშნო ლაპლასიანის მიხედვით გამოსახვა იოლ ამოცანას წარმოადგენს, ხოლო ამ უკანასკნელის  ქვეგრაფების მიხედვით შეფასების პრობლემის ამონახსნი ერთ-ერთი ჩვენგანის მიერ ადრე გამოქვეყნებულ ნაშრომშია მოცემული [12]:

κ₁ = 2m     (24a)

κ₂ = 4m + 2|K_1,2|   (24b)

κ₃ = 8m + 12|K_1,2| + 6 |K_1,3| + 6 |C₃ |   (24c)

   (24d)

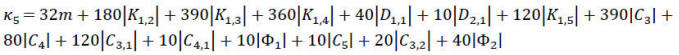       (24e)

ამ გამოსახულებებში ქვეგრაფები სტანდარტული ნოტაციით არის მოცემული.

პრაქტიკული თვალსაზრისით მოსახერხებელია (23) განტოლების გამარტივება. თუ გავიხსენებთ, რომ ნაჯერი ნახშირწყალბადების შესაბამისი გრაფების წვეროების ხარისხებს შორის უდიდესი არ აღემატება ნახშირბადის ვალენტობას (ოთხს), შეგვიძლია, დავასკვნათ, რომ Γ მატრიცის წამყვანი საკუთარი მნიშვნელობა არ აღემატება ათს (2Δ+2, სადაც Δ≤4); ამრიგად, იმ დათქმით, რომ ω₁≈10, ხოლო ξ₁≈8, ვღებულობთ რნბ-მატრიცის დეტერმინანტის ათობითი ლოგარითმის შემდეგ მიახლოებით გამოსახულებას:

GG^(r) ≈ GG^(r) + lg 10ⁿ = GG - n                (25)

გავითვალისწინოთ, რომ

U ≈ 10^-1 (Q - 8I_n)     (26)

და, შესაბამისად,

υ_i ≈ 0.1 (ξ_i - 8)   (27)

ნათელია, რომ ნაჯერი ნახშირწყალბადების U= Γ^(r)  - I მატრიცების აპროქსიმაციის სპექტრული რადიუსი  -0.8≤υ≤0 ინტერვალშია, ხოლო მათი დაყვანილი Γ^(r) მატრიცისა - [0.2;1]. შესაბამისად, ამ უკანასკნელის ნატურალური ლოგარითმი კვლავინდებურად  რეალური რიცხვებისაგან შედგენილ მატრიცას წარმოადგენს.

ზემოთქმულიდან გამომდინარეობს, რომ

 

 

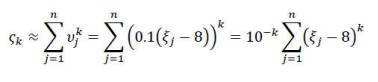
და

 

 

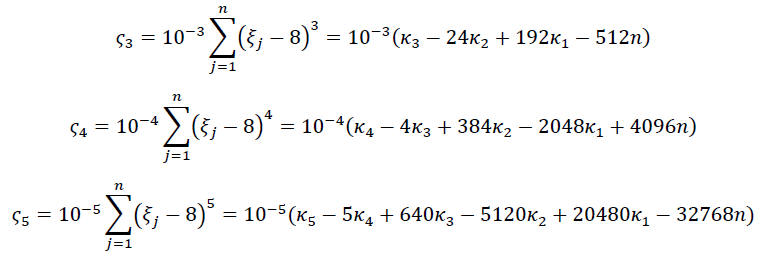
სადაც κ_i უნიშნო ლაპლასიანის i-ური სპექტრული მომენტია.

ამრიგად ვღებულობთ:

Tr (ln Γ ^r)) ≈ 0.000002κ₅ - 0.00004κ₄ + 0.0005κ₃ - 0.0328κ₂ + 0.3362κ₁ - 1.4589n

და

GG^(r) = Tr (lnΓ^(r)) / ln10 ≈ 0.0000008κ₅ - 0.000017κ₄ + 0.0002κ₃ - 0.0142κ₂ + 0.1460κ₁ - 0.6336n

რადგან  GG = n + GG^(r),

GG ≈ 0.0000008κ₅ - 0.000017κ₄ + 0.0002κ₃ - 0.0142κ₂ + 0.1460κ₁ + 0.3663n  (28)

და (28) განტოლებების კომბინაციით ვღებულობთ ამონახსნს:

GG ≈ 0.3663n + 0.2366m - 0.0267|K_1,2| + 0.0005|K_1,3| - 0.000036|D_1,1| - 0.0005|C₃ | - 0.00012|K_1,4| - 0.00004|C_3,1| - 0.000072|C₄| + 0.000008|D_2,1| + 0.000096|K_1,5| + 0.000008|C_4,1| + 0.000008|Φ₁| + 0.000008|C₅| + 0.000016|C_3,2| + 0.000032|Φ₂|               (29)

მიღებული განტოლების ავტორების მიერ ადრე შემუშავებული მეთოდების [13, 14, 15] საფუძველზე განზოგადება ჰეტეროატომების შემცველი სისტემებისათვის შემდგომ ამოცანას წარმოადგენს.

 

დასკვნა

მიღებული შედეგები ცხადყოფს, რომ რნბ-მატრიცის დეტერმინანტის ლოგარითმის კორელაციები ნივთიერებათა ფიზიკურ-ქიმიურ თვისებებთან და ბიოლოგიურ აქტივობებთან წარმოადგენს არა შემთხვევითობას, არამედ განპირობებულია ხსენებული მოლეკულური დესკრიპტორის ცალსახა დამოკიდებულებით მოლეკულებში არსებულ ფუნქციურ ჯგუფებზე. მიღებული განტოლებების განვრცობა უფრო მაღალი რიგის წევრებით სავსებით შესაძლებელია, წარმოადგენს რა მხოლოდ ტექნიკურ საკითხს, მაგრამ, პრაქტიკული თვალსაზრისით, მნიშვნელობა გააჩნია მხოლოდ ისეთი სისტემების მოდელირებისას, როგორებიცაა, მაგალითად, ბიომაკრომოლეკულები, ცეოლითები და სხვა.

აღსანიშნავია ის გარემოებაც, რომ (23) განტოლების პირველი წევრი (lgω₁ⁿ) წარმოადგენს ენტროპიის ანალოგიურ ფუნქციას. გარდა ამისა, აღნიშნული განტოლების გამოყენება შესაძლებელია ისეთი ემპირიული დამოკიდებულებების დასაბუთებისა და დაზუსტებისათვის, როგორებიცაა, მაგალითად, ტრუტონის, ვალდენისა და დიუკლო-ტრაუბეს წესები.

 

ლიტერატურა

[1]. მ. გვერდწითელი, გ. ჩაჩავა, ი. გვერდწითელი, “კორელაციის ‘აღნაგობა-თვისებები’ გამოკვლევა რნბ-მატრიცების მეთოდის ფარგლებში II მთავარი ქვეჯგუფის ელემენტთა ქლორიდებისათვის”, საქ. ქიმ. ჟურნალი, ტომი 5, No 1, გვ. 63, 2005.

[2]. გ. ლეკიშვილი, გ. ცინცაძე, გ.ნ. ჩაჩავა, მ. გვერდწითელი, გ.გ. ჩაჩავა, “ბინარული ნაერთების კრისტალური სტრუქტურების მათემატიკური დახასიათება”, საქ. ქიმ. ჟურნალი, ტომი 1, No 1, გვ. 54-55, 2001.

[3]. M. Gverdtsiteli, G. Lekishvili, “Mathematical-Chemical Investigation of some Straight-Chain Alkyl Mono-Halides”, Bull. Georg. Nat. Acad. Sci., Vol. 5, No 1, pp. 58-59, 2011.

[4]. M.G. Gverdtsiteli, G. Otinashvili, M. Bedianashvili, M. I. Gverdtsiteli, N. Ovsianikova, “Algebraic-Chemical Investigation Monocarbon Acids within the Scope of Quasi-ANB-Matrices Method”, Georg. Chem. Journal, Vol. 3, No 3, p. 244, 2003.

[5]. ნ. სიდამონიძე, რ. ჩიქვინიძე, მ. გვერდწითელი, “1-S-ცისტეილაცეტოგლუკოზის სინთეზის რეაქციის ალგებრულ-ქიმიური შესწავლა ქვაზი-რნბ-მატრიცების მეთოდის ფარგლებში”, საქ. ქიმ. ჟურნალი, ტომი 2, No 1, გვ. 171, 2002.

[6]. V. Mnukhin, “A Basis of the Algebra of Graph Invariants (In Russian)”, In: Mathematical Analysis and Applications, Rostov-na-Donu: RGU Press, 1983, pp. 55-60.

[7]. I. Baskin, M. Skvortsova, I. Stankevich, N. Zefirov, “On the Basis of Invariants of Labeled Molecular Graphs”. J. Chem. Inf. Comput. Sci., Vol. 35. pp. 527-531, 1995.

[8]. E. Estrada, M. Benzi, “What is the meaning of the graph energy after all?” Discrete Applied Mathematics, Vol. 230, pp. 71-77, 2017.

[9]. N. J. Higham, Functions of Matrices: Theory and Computation, Philadelphia: SIAM, 2008, 450 p.

[10]. D. Cvetković, P. Rowlinson, S. Simić, An Introduction to the Theory of Graph Spectra, Cambridge: Cambredge University Press, 2010, p. 217.

[11]. D. Cvetković, P. Rowlinson, S. Simić, “Eigenvalue Bounds for the Signless Laplacian”, Acad. Serbe Sci., Publ. Inst. Math., Vol. 81(95), pp. 11-27, 2007.

[12]. G. Lekishvili, “Evaluation of Spectral Moments of Signless Laplacian on the Basis of Sub–Graph Contributions and Their Applications to the Zagreb Group Indices”, MATCH Commun. Math. Comput. Chem. Vol. 75, pp. 355-363, 2016.

[13]. გ. ლეკიშვილი, ლ. ასათიანი, მოლეკულური დესკრიპტორები ელემენტორგანულ ქიმიაში, თბილისი: თსუ, 1998, გვ. 30-37.

[14]. I. Gutman, J.-Y. Shao, “ The Energy Change of Weighted Graphs”, Linear Algebra and its Applications, Vol. 435, No 10, pp. 2425-2431, 2011.

[15]. I. Gutman, “Topological Studies on Heteroconjugated Molecules. VI. Alternant Systems with Two Heteroatoms”, Z. Naturforsch., Vol. 45a, pp. 1085-1089, 1990.

 

Recieved: 21-04-2021 | Web published: 11-05-2021 | Views 495